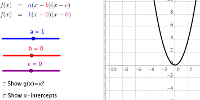|
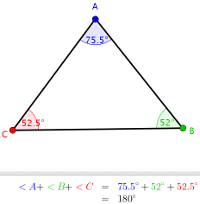
Absolute Value
- Show how the graphs of \( f(x) \) and \( |f(x)| \) relate to each other
- Choose from:
- \( f(x)=a(x−b) \)
- \( f(x)=a(x−b)(x−c) \)
|

|
Absolute Value - Draggable
- Show how the graphs of \( f(x) \) and \( |f(x)| \) relate
to each other
- \( f(x) \) is defined by draggable points
- Choose from:
- \( f(x)=ax+b \)
- \( f(x)=ax^2+bx+c \)
|

|
Linear - \( y = mx + b \)
-
Show how the parameters in \( y = mx + b \) are related to the characteristics of the corresponding graph
|

|
Quadratic - Expanded Form
-
Show how the parameters in \( f(x)=ax^2+bx+c \) are related
to the characteristics of the corresponding graph
|
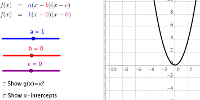
|
Quadratic - Factored Form
-
Show how the parameters in \( f(x)=a(x−b)(x−c) \) are related
to the characteristics of the corresponding graph
|
|
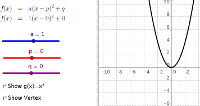
Quadratic - Vertex Form
-
Show how the parameters in \( f(x)=a(x−p)^2+q \) are related
to the characteristics of the corresponding graph
|
|
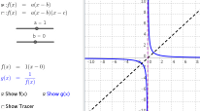
Reciprocal - Polynomials
-
Show how the graphs of \( f(x) \) and \( \frac{1}{f(x)} \)
relate to each other
- Choose from:
- \( f(x)=a(x−b) \)
- \( f(x)=a(x−b)(x−c) \)
|

|
Reciprocal - Polynomials - Draggable
-
Show how the graphs of \( f(x) \) and \( \frac{1}{f(x)} \)
relate to each other
- f(x) is defined by draggable points
- Choose from:
- \( f(x)=ax+b \)
- \( f(x)=ax^2+bx+c \)
|

|
Stretches - Practice
-
Given a random function and a random stretch of that function
(of the form \( g(x)=af(bx) \) ), determine what
\( a,b \) must be
-
Watch the individual stretches to see if your \( a,b \) values are
correct
- Keep practicing with random functions
|

|
Transformations - Animation
-
Enter values for \( a,b,h,k \) and click buttons to watch
the individual transformations of \( g(x)=af(b(x−h))+k \)
separately
-
For negative \( a \) and \( b \) values, watch the stretch,
then see the reflection
- Also see how a moveable point gets transformed
-
Choose from the following functions:
| \( f(x)=x \) |
\( f(x) = x^2 \) |
| \( f(x) = x^3 \) |
\( f(x) = \sqrt{x} \) |
| \( f(x) = 10^x \) |
\( f(x) = \log_{10}{x} \) |
|

|
Transformations - Animation - Piecewise
-
Enter values for \( a,b,h,k \) and click buttons to watch the
individual transformations of \( g(x)=af(b(x−h))+k \) separately
-
For negative \( a \) and \( b \) values, watch the stretch,
then see the reflection
-
\( f(x) \) is a piecewise function defined by draggable points
|

|
Transformations - Practice
-
Given a random function and a random transformation of that
function (of the form \( g(x)=af(b(x−h))+k) \), determine what
\( a,b,h,k \) must be
-
Watch the individual transformations to see if your \( a,b,h,k \)
values are correct
- Keep practicing with random functions
|

|
Transformations - Sliders
-
Use sliders to show how the graph of \( g(x)=af(b(x−h))+k \)
is related to the graph of \( f(x) \)
- Also see how a moveable point gets transformed
-
Choose from the following functions
| \( f(x)=x \) |
\( f(x) = x^2 \) |
| \( f(x) = x^3 \) |
\( f(x) = \sqrt{x} \) |
| \( f(x) = 10^x \) |
\( f(x) = \log_{10}{x} \) |
|

|
Transformations - Sliders - Piecewise
-
Use sliders to show how the graph of \( g(x)=af(b(x−h))+k \)
is related to the graph of \( f(x) \)
-
\( f(x) \) is a piecewise function defined by draggable points
|

|
Translations - Practice
-
Given a random function and a random translation of that
function (of the form \( g(x)=f(x−h)+k) \) , determine what
\( h,k \) must be
-
Watch the individual translations to see if your \( h,k \)
values are correct
- Keep practicing with random functions
|